已知:如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,AD中点,求证:四边形EFGH为平行四边形。
分析:当题中有中点时,特别是有两个中点时,如果中点在一个三角形中,直接用三角形中位线定理;如果不在一个三角形中,则需要连结四边形的对角线,构造三角形,再利用三角形中位线解答问题。
证明:连结AC
∵E,F分别是AB,BC中点,
∴EF//AC且EF=1/2AC
同理HG//AC且HG=1/2AC
∴EF//HG且EF=HG
∴四边形EFGH为平行四边形。
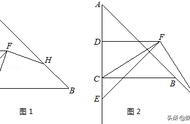
例2、如图:在△ABC中,延长BC至D,
使CD=1/2BC,过AC的中点E作EF//CD(点F位于点E右侧)且EF=2CD,连接DF,若AB=8,则DF长为( )
A,3 B,4 C,2√3 D,3√2

分析:延长FE交AB于点M,则M为AB中点。从而可得BD=MF,又因为EF//CD,可得BDFM为平行四边形,从而得
DF=BM=1/2AB=1/2×8=4
三、三角形中位线常见题型。
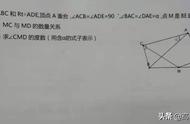
例1、(2019,湖州中考题)如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连接DF,EF,BF。
(1)求证:四边形BEFD是平行四边形
(2)若∠AFB=90°,AB=6,求四边形BEFD的周长。

证明:(1)∵D,F为AB,AC中点
∴DF//BC,同理EF//AB
∴四边形BEFD为平行四边形。
解(2)∵∠AFB=90°,又∵D为AB中点。
∴DF=1/2AB=1/2×6=3(直角三角形斜边上的中线等于斜边的一半。这一定理在矩形性质一节)
BD=1/2AB=1/2×6=3
∴平行四边形BEFD周长=2×(3 3)=12
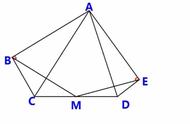
例2、在△ABC中,M是BC的中点,AD平分
∠BAC,BD丄AD于点D,AB=10,AC=14,
求DM的长。

分析:当题中只有一个中点时,需要添加辅助线,构造三角形的中位线。因为AD丄BD,且平分∠BAD可得△BAE为等腰三角形,D为BE中点。
解:延长BD交AC于点E。
∵AD丄B,AD平分∠BAC
∴△BAE为等腰三角形
∴AE=AB=10,D为AE中点
∴CE=AC-AE=14-10=4
∵M为AC中点,D为AE中点
∴DM=1/2CE=1/2×4=2
敬请关注,持续更新中。
,