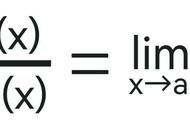这不就是刚才拉格朗日中值定理的别墅二层小楼形式么,所以这里就不过多解释
柯西中值定理是拉格朗日中值定理的推广,是微分学的基本定理之一。其几何意义为,用参数方程表示的曲线上至少有一点,它的切线平行于两端点所在的弦。该定理可以视作在参数方程下拉格朗日中值定理的表达形式。
柯西中值定理粗略地表明,对于两个端点之间的给定平面弧,至少有一个点,弧的切线通过其端点平行于切线。
与拉氏定理的联系在柯西中值定理中,若取g(x)=x时,则其结论形式和拉格朗日中值定理的结论形式相同。
因此,拉格朗日中值定理为柯西中值定理的一个特例;反之,柯西中值定理可看作是拉格朗日中值定理的推广。
证明:
若令u=f(x) , v=g(x),这个形式可理解为参数方程,而f(b)-f(a)/g(b)-g(a)则是连接参数曲线两端点弦的斜率,f'(ξ)/g'(ξ)表示曲线上某点处切线的斜率,在定理的条件下,结论可理解如下:

用参数方程表示的曲线上至少有一点,在这一点处的切线平行于连接两个端点的弦。
应用例子1.泰勒公式柯西中值定理最主要的应用是证明带有拉格朗日余项的n阶泰勒公式,只要反复使用柯西中值定理多次就能证明,下面以n=1为例说明。
例 1
设f(x)在(a,b)内二次可微,证明:任意的x , x0∈(a,b),在x , x0之间存在ξ,使

这就是函数f(x)在点x0邻域内的一阶泰勒公式。
证明:令