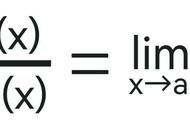G(x)=(x-x0)²利用

在两次应用到柯西中值定理后可以得到:

命题得证。
2.洛必达法则柯西中值定理的一个最重要的应用就是可以推导计算待定型的极限最有效的方法——洛必达法则。
洛必达法则是求两个无穷小量或两个无穷大量的比的极限。在满足一定条件下可以化成两个函数的导数的比值极限,这样就有可能使得原待定型变成简便而有效的求非待定型极限的问题。
我们得出下面这个定理(洛必达法则):
⑴ 两个函数f(x)和g(x)在开区间(a,b)可微,并且在这个开区间上,g(x)的导数不等于0;
⑵ 存在极限

其中A为一个有限的常数。则在以下情况下: