第三、数量积公式的应用
在空间中,数量积公式主要应用于探求点的坐标、位置,证明线线垂直、线面垂直、求异面直线夹角等。
如下是相关证明依据:

通过以上,大家可以看到,我们证明线面问题的时候,必然会涉及到平面的法向量问题,我们在看几个例子,通过这些原理来透彻理解空间向量在立体几何里面的应用:
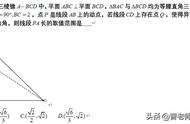
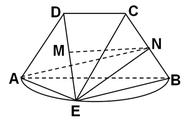
一、求线面角问题:
线面角定义:线和它在面中的射影所成的角,

示例如下:

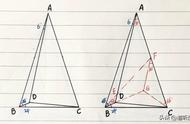
二、求点到面的距离问题:

第三、数量积公式的应用
在空间中,数量积公式主要应用于探求点的坐标、位置,证明线线垂直、线面垂直、求异面直线夹角等。
如下是相关证明依据:

通过以上,大家可以看到,我们证明线面问题的时候,必然会涉及到平面的法向量问题,我们在看几个例子,通过这些原理来透彻理解空间向量在立体几何里面的应用:
一、求线面角问题:
线面角定义:线和它在面中的射影所成的角,

示例如下:

二、求点到面的距离问题:












Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.