解答过程:
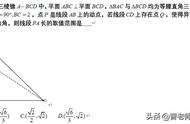
建立如上图所示的空间直角坐标系 A-xyz ;
则 A(0,0,0),D(1/2,0,0),C(1,1,0),S(0,0,1);
设向量 n1 = (x,y,z)是面 SCD 的法向量,则有:n1⊥DC , n1⊥SD ;
∵ 向量 DC = (1/2,1,0),向量 SD = (1/2,0,-1),

∴ 平面 SCD 的法向量 n1 = (2,-1,1),
易知面 SAB 的法向量 n2 = 向量 AD = (1/2,0,0),

所以所求锐二面角的余弦值为 √6/3 。
例题2、四边形 ABCD 为正方形,PD⊥平面 ABCD ,PD∥QA ,QA = AB = 1/2 PD 。
(1)证明:平面 PQC⊥平面 DCQ ;
(2)求二面角 Q-BP-C 的余弦值 。

解答过程: