这样一来,“切”似乎与“割”或者“切割”没啥不同?
非也!其实,即使不在讨论切线的语境中,“切”的意思也远非上述这些,它还有“贴近”和“契合”之意,表示刚好靠近,而未越过界限进入对方内部。词语诸如“贴切”、“切中”等皆由此而生。而“切线”一词,正是取此义而得也。
假设此刻你脸上有一只蚊子,而我又是一位武艺高强手握双板斧的大咖,我将会用利斧贴着你的脸皮掠过,斧口掠过的路径就是一条切线,你将毫发无损,而位于切点的蚊子被准确的砍死。
讲了这么久,你现在明白了上面那个切线定义的由来吧!
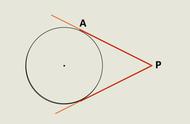
按照这种切线的定义,考虑如下图这些情况。

显然, , 和 都发生了切割,所以那些红线都是割线。而 中只是发生了切,与割不同的是,即使因此而切掉了一点,也可忽略,因为数学上的点本来就没大小嘛!因此,曲线没有因为切线的切而断掉。
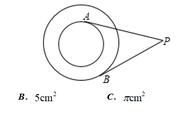
当然,机智如你,有人提出,按此上面这种理解方式,下面这种也是切线,理由是二者有接触,曲线未被切割。对吗?

不对不对!切线应该是直线,而你这里是射线嘛。
关于切线的这样的一种观点或约定,一直被广泛的接受,直到1828年。
因为不断有人提出:一条切线应该只与曲线上一个点关联,而不必管它是否在别的位置切割曲线。按此说法,像上图 中的红线也应该是切线!
也就是说,对曲线有转向的情况,因为无法避免直线与曲线切割,上面所提到的切线定义无法给出切线。
所以,1828年以后,这种频繁出现在各种词典中的定义被正式宣布废弃了。
如果你还持有这种观念,那很抱歉,你的观念已经out快两百年了!
1828年之后,词典里对切线的给出的定义是:
切线指的是一条刚好触碰到曲线上某一点的直线。
实际上,“切线”一词的英文——“tangent”,源自拉丁语“to touch”,表示接触的意思。窃以为,这种接触就是点到为止,不过分依靠和攀附。
据此描述,对于将切线演示出来这件事,具有良好的可操作性:当你拿着一根不太长的直线靠近曲线上的某个确定点时,只要让你手里的直线与曲线刚好接触,你手里的直线就是那条要找的切线。
若你将一根刚性直杆搭在一个圆球上,只要你避免杆的两端与球面直接接触,可以肯定,杆必定与球保持相切。
如下图,假设地面光滑,左边的球与墙壁接触但无压力,因此球没有发生形变,所以墙面和球面刚好接触,二者相切。而右边的球因为受到细线的斜拉力,必定受到墙面的支持力,球面发生形变,它与墙之间并非点到为止,因此墙面不是球面的切面。

虽然这种切线定义是正确的,并且实际操作性强。但这句话有点模糊,“刚好触碰”什么意思?感觉正经的数学定义不会这么说,的确不太好理解,所以这个定义的接受度不是很高。
为了解决广大群众对数学知识的向往与有限的理解力之间的矛盾,人们需要一种更浅显的说法。比如:有几个交点就算切线?于是,“只交于一点”这么一个最直观,但却很容易找到反例的错误说法依然占有较大的市场。
难道在漫长的人类文明史中,切线的定义就只是这个?
非也!太小看历史上的那些聪明的数学家了!其实早在古希腊时代,人们就给出了准确的定义,后来人们又对切线给出多种定义。但遗憾的是,或许是因为数学和几何上的严格定义往往是比较抽象的,这些正确定义并未被大众所熟知。
那么,到底有哪些大牛曾经提出过正确的切线的定义呢?其实,古希腊的数学家欧几里德和阿基米德、比牛顿稍早的法国数学家费马以及牛顿本人等,都对切线做过研究。本文无意去地毯式探求切线定义的发展历史,只列举一下最为重要的两个定义。
第一个定义来自古希腊三大数学家之一的阿波罗尼奥斯(Apollonius of Perga,约公元前262~190)。