在数学中,喇叭角,也称为horn angle,是一种曲线角,定义为两条相切的曲线之间形成的角。下面这只牛角表面沿纵向正对的两条曲线近似牛角尖处相切,因此就形成一个喇叭角。当然,你可能会钻牛角尖,因为牛角是个立体角。

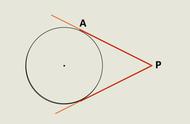
按照阿波罗尼奥斯的观点,若切线为直线,那么,切线与曲线之间形成的喇叭角是经过该点所有直线与曲线形成的角中最小的那一个。
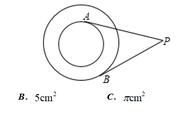
当然,如果切线没有被限制为直线,那么在它与所切的曲线之间,可以插入另外的不同曲线,它们之间彼此两两相切。例如下图中, 就成功的被插入到 和它的切线之间。

阿波罗尼奥斯将切线定义为一条直线,那么它和曲线之间不可能还能插入其他的直线。话句话说,所谓切线就是那个与曲线接触并形成最小夹角的直线。
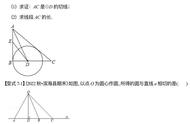
不过,值得注意的是,这种切线的定义只适合于光滑的曲线,如果像下面这种情形,切线是不存在的。图中红色的直线只是曲线部分的切线,而非整体的切线。

阿波罗尼奥斯不愧为几何学大师,给出的切线的定义似乎无懈可击。即使将切线推广至曲线,也是可以的。因为若切线是形状大小固定曲线,当你试图将另一条同样的曲线插入喇叭角,并使它同一位置与切点重合时,它必然与原来的切线重合。换句话说,切线和曲线之间也无法再插入一条(同样的)切线了。
但事实上,将切线限定为直线也是合理的。
这样做,并不妨碍研究两个曲线相切这件事。因为曲线是否相切可以根据它们在某个公共点上是否共有切线来判定。事实上,我们就是这么做的!不光如此,人们还规定,当两个曲线在一个公共点的切线互相垂直时,我们就说这两个曲线正交。
设圆与一曲线相切,若圆在曲线的凹的一侧,且曲线在切点处的曲率半径等于圆半径,则该圆称作曲线的密切圆,如下图所示。