8 描述无穷大
无穷数学的奠基者康托尔提出:如果两个无穷集合可以一一对应,那么就称其是等势的,且它们有相同的基数,我们可以用希伯来字母(alehp,读作阿列夫)来描述基数的大小,字母右下方的角标代表“无穷大”的“等级”:
现在我们可以说:整数的数量是,一条线段上点的数量是,就像平时我们说:嘿,这有3个苹果,那有2支笔这么简单。
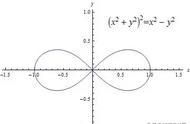
事实上,数学家发现,几何曲线的种类大于实数的数量,因此我们可以用描述几何曲线的所有种类。正如人类在浩瀚的宇宙面前惊叹于自己的渺小,在数学中,也有比无穷大更大的无穷大,真是令人感到惊异。

参考文献[1](美)乔治·伽莫夫.从一到无穷大[M].阳曦译.天津人民出版社,2019.[2](美)R·柯朗,H·罗宾. 什么是数学——对思想和方法的基本研究[M].复旦大学出版社,2012.
来源:大小吴的数学课堂
编辑:aloysius
1. 2. 3. 4. 5. 6. 7. 8.
10.