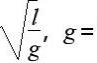所以在算周期时这两段得分开来算,在这段运动的摆长是l,实践就是π乘根号线lbg,这段运动的摆长是二分之l,实践就是π乘根号线l比二g,周期就是它俩的和,这就算出来了。看来若单摆在摆动过程中摆长有变化就得分段去算时间再求周期。

除了这些单线或多线的单摆,还有一种类单摆运动的模型是长这样的,小球在光滑球面aoc上来回运动,它的受力情况就类似于单摆运动,小球做的自然就是简协运动,它的周期也满足公式二ππ乘以根号下lbg。
这个l指的就是圆弧的半径,一般用r表示,利用这个模型来看一道小弱题,光滑圆弧面ao与水平面相切于o点,将一小球从湖面顶端a释放,另一等大的小球从b释放。你知道两次到达o的时间关系吗?要研究时间就得看周期吗?刚才说过这种运动就可以看成单摆运动,所以周期就用这。显然不管小球从哪里释放,这个半径都是2,所以周期必然相等。它们从a或b运动到o都经历四分之一周期,所以到达o点的时间自然就相等了。

以后遇到这种光滑圆弧类问题一定要想到它可以看成间歇运动,在分析时间时就利用单百的周期去算。

这个视频就给你讲了周期和摆长的关系,不管魔性如何变化,解题的关键都在于找到等效摆长,其中若摆长有变化得分开来算。另外遇到这种光滑圆弧的运动要立马反应过来,它就是逆蛋白运动,算周期就用这个式子来算。
都明白了吗?明白了就去刷题闯关去吧。
,