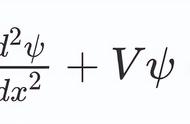我们知道频率与波长有关。这里c 是光速。采用相对论的结果,我们可以将光子的能量与动量联系起来。综合上述结论可给出在光子的波长 λ与动量 p之间的关系式:

其中h为普朗克常数。
基于此,德布罗意假设波长与动量之间的关系式应该对于任何粒子都成立。此时,最好先放弃你的直觉,不去想表现的像波的粒子究竟意味着什么,而是仅跟着数学的逻辑走下去。
在经典力学中,波(比如声波和水波)随时间的演化,可用波动方程来描述:其是一个微分方程,解为波函数,可以给出在任意时刻服从恰当边界条件的波的形状。
举例来说,假设波沿在x方向延伸的弦传播,在xy平面内振动。为了完全描述这个波,你需要知道在每个点x每个时刻t弦在y方向的位移。利用牛顿第二运动定律可知遵循如下波动方程:

v为波速。

上图为在xy平面内弦振动的照片,这里的波可被余弦函数所描述。
上述方程的一般解相当复杂,反映出弦可以根据各种方式进行摆动的事实。并且你需要更多的信息(初始条件和边界条件)来搞清楚到底是哪种运动。但是,作为一个例子,