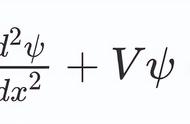这些方程可应用于在三维空间运动的单粒子,对于有任意粒子的系统,也有相应的方程来描述。如果不把波函数写成位置和时间的函数,人们也可以将它们化为动量和时间的函数。
进入不确定性
我们可以从一个简单的例子(比如在无限深势阱中运动的单个粒子)出发来求解薛定谔方程,它的解与描述一个波的数学方程非常相似。
这个解到底意味着什么?它并不会给出粒子在给定时刻的精确位置,也不会给出一个粒子随时间变化的轨迹。更确切的说,它在给定时间的所有可能位置(x,y,z)可以给出你一个值ψ(x,y,z,t)。这个值意味着什么?在1926年时,物理学家波恩(Max Born)提出了统计诠释。他假设,波函数绝对值的平方


这个概率图像与德布罗意关于粒子波长和动量关系公式有令人吃惊的联系。海森堡在1927年发现,如果要测量一个运动粒子的位置和动量,人们有一个基本的精度限制。在某一方面如果想要测量的精度越高,其他方面人们能说的就越少。这并不是指测量仪器的质量问题,而是自然界根本就具有的不确定性。这个结果现在称为海森堡的不确定性原理,且是常常用来引述量子力学奇怪现象的几个结果之一。它意味着在量子力学里我们谈论不了粒子的位置或轨道。

海森堡(Werner Heisenberg), 1901-1976.
“如果我们相信不确定性图像,由于我们对于像‘电子在时刻在哪里’这样的问题没有明确的答案,换句话说,所有量子状态的数学表示和状态都只能给我们概率的结果”,布瓦塔说。“德布罗意、薛定谔和爱因斯坦尝试提供一个真实的诠释,比如:在真空中传播的光波。但是,还有一些物理学家,泡利、海森堡和玻尔反对给出现实的图像。对于他们而言,波函数仅仅是计算概率的一个工具。”
它真的适用么?
为什么我们要相信这个异想天开的想法呢?在这篇文章中我们已经展示了薛定谔方程,好像它是从空中生拉硬拽出来的,但是它实际来自于哪里呢?著名的物理学家理查德.费曼认为这是个无意义的问题:“我们从哪里得到这个方程?它不能由你所知道的任何知识来推导出来。它来自于薛定谔的大脑。”
然而,这个方程已经经受住了迄今为止的每一个实验的考验。“这是量子力学中最基本的方程”,布瓦塔说,“这是我们想要描述的所有量子力学系统(如:电子、质子、中子等系统)的出发点。”这个方程早期成功地描述了氢原子的离散能谱,促成了量子力学的建立,这也是薛定谔的动因之一。根据欧内斯特·卢瑟福的原子模型,像氢原子这样的原子所发出的光的频率应该是连续的。然而实验表明:它并没有连续变化,氢原子只放出特定频率的光,当频率改变时有跳跃。这个发现与传统的哲学智慧背道而驰,传统的哲学思想是支持由十七世纪的哲学家和数学家戈特弗里德·莱布尼茨所说的格言的:“大自然不会跳跃(nature does not make jumps)”。
在1913年尼尔斯·玻尔提出了一个新的原子模型,在这个模型中,电子被限制到了特定的能级。薛定谔将它的方程应用于氢原子,发现他的解精确重复了由玻尔设定的能级。“这是一个激动人心的结果,也是薛定谔方程最初的主要成就之一”,布瓦塔说。
由于无数成功实验的支持,薛定谔方程在量子力学中已成为牛顿第二定律的类似物和替代品。
原文来源:https://plus.maths.org/content/schrodinger-1
互动问题
【互动问题:假如你的猫被薛定谔捉走了,要求你说出自己对量子力学的理解才能放猫,你会说什么?
】
请大家严格按照 互动:问题答案的格式在评论区留言参与互动,格式不符合要求者无效。
截止到本周四中午12点,点赞数前三名的朋友将获得我们送出的图书一本。
编辑:aki