圆周率π
公元前3世纪,古希腊数学家阿基米德通过圆内接和外切正多边形逼近圆周的方法得到圆周率介于 3(10/71)和 3(1/7)之间。我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率,并指出在圆的内接正多边形加倍的过程中“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”。他计算出π≈157/50≈3.14。南朝的祖冲之又进一步求得π的值在3.141 592 6和3.141 592 7之间,是第一个将圆周率的计算精确到小数点后7位的人。
弧长和扇形面积

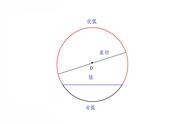
弧长
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。

扇形的面积

圆锥的侧面积与全面积