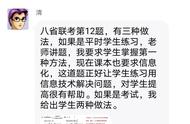
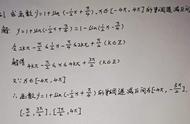第三个解法属于求出平移伸缩后整体的单调减区间,再把(π/2,π)卡到减区间内即可,此时的单调区间有无数个,需对k进行赋值,常规验证k=0,k=1,k=-1,但很多时候所需赋值能直接看出,没必要挨个验证,这种方法不如方法二,不推荐使用。

第四个解法从导数的角度入手,将单调转化为三角函数在区间内非负或非正,再从解三角不等式的角度入手即可,如果熟知单位圆和三角函数线在三角函数中的应用,这种方法反而是最容易的一种。

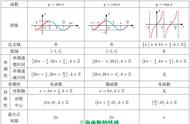
以上四个方法均可使用,但推荐先确定区间长度和半个周期的大小后换元赋值,即上述第二种解法,与单调性有关的参数范围求解难度不大,理解解题原理即可,给出一道挺不错的相关案例题:

这个题只是把上述已知的φ用任意性表示而已,解法和上述相同,只是多了一步用任意性消去φ的过程,由于题目中并未告知ω的正负,所以换元时需要分三个情况讨论,题目难度不大,过程如下: