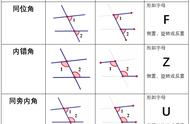
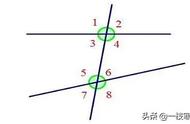
条件:AB∥CD,O为BC的中点.
结论:△AOB≅△DOC.
将军饮马
链接:初中几何最值问题基本模型:将军饮马
模型1:定直线与两定点(一动两定型)
(一)距离之和最短(化折为直)
1.两侧型:两点分别在直线两侧(基础本质型)

已知:如图①,定点A、B分别位于直线L的两侧.
要求:在直线L上找一点P,使得PA PB的值最小.
作图:连接AB与直线L交于点P,点P即为所求作的点,PA PB的最小值即为线段AB的长度.
证明:在直线L上任取一点动点P',连接AP',BP'.
在△ABP'中,
∵AP' BP'≥AB,即AP' BP'≥PA PB,
∴当线段AB与直线L相交于点P时,PA PB最小.
结论:PA PB最小(AB)
2.同侧型:两点在直线同侧(将军饮马)

已知:如图①,定点A、B位于直线L的同一侧.
要求:在直线L上找一点P,使得PA PB的值最小.
作图:作点A、B任意一点关于直线L的对称点,
连接AB'交直线L于点P,则点P即为所求.
证明:根据轴对称的性质知直线L为线段BB'的中垂线,
由中垂线的性质得PB=PB',要使PA PB最小,则需PA PB'最小,从而转化为两侧型.
结论:PA PB最小(AB').
(二)距离之差的绝对值最大
1.同侧型:

已知:如图①,定点A、B位于直线L的同一侧(A、B两点到L的距离不等).
要求:在直线L上找一点P,使得|PA-PB|的值最大.
作图:连接AB并延长,与直线L交于点P,点P即为所求.
证明:在L上任取一点P'(异于点P),连接P'A,P'B.由三角形三边关系知|P'A-P'B|<AB,即|P'A-P'B|≤|PA-PB|.
结论:|PA-PB|最大(AB).
2.同侧型: