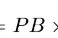是的,所有的三角形都可以通过面积=(1/2)·底·高来计算它的面积。
但是底与高的关系依赖于三角形的形状,所以它们的面积系数也会有差异。

为什么我们需要相似性来保证它们可以使用相同的面积公式呢?
直觉告诉我们,我们等比例缩放一个图形时,绝对大小会改变,但是比例却不会发生改变。
一个正方形,无论它怎么缩放,都有周长=4*边长。
因为面积系数的选择基于图形的比例,所以任何拥有相同比例的图形都可以通过同一公式来计算面积。
这有些像所有人的臂展都近似等于身高。
不管他是NBA球员还是一个孩子,他们都可以使用相同的公式因为他们都是相关的。

我希望这些更高级的概念能够说得通:
- 面积可以从任何线段的平方中得到,而不只是从边长或半径中
- 每一个线段都有相应的“面积系数”
- 相似的图形可以使用同一面积公式

但是有人会问:为什么相似的图形拥有一样的面积系数呢?
以下是我的理解:
成比例的图形拥有相同的比例。为什么呢?当我们移动一个物体,显然它的大小会发生改变(比如说一个停止标志靠近或走远),但是它的比例不会发生变化。一个物体有可能知道它正在被远处的人观察,因而去改变自己的边长与面积的比例吗?考虑两个相似的图形。把大的移动到远处,直到看起来它的大小与小的图形相等。现在它们看起来一样了,因此它们拥有相同的比例关系(比如说周长与面积)。现在拉动大的图形,它看起来更大了。但是在移动的过程中,它的比例关系并没有发生变化——它们就跟小图形的比例关系一样。