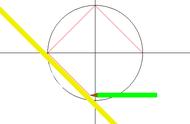
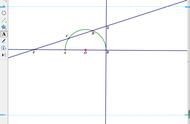
这是一位读者(Per Vognsen)更加正规的证明:
你只需要证明对于一类相似图形,L² /A是一个常数即可。在一类相似图形中任意选取两个图形,它们的面积分别是A与A' ,长度分别是L与L' 。令F是把一个图形映射到其他图形上的缩放系数。然后我们就得到A = F² * A',L = F * L' 。把长度平方即可得到 L²= F² * L'² 。面积方程除以该等式,F²便可以被消掉,同时得到A/L² = A/L'²。所以便可知面积与长度平方的比例确实为一常数。
直觉化的看待毕达哥拉斯定理
我想我们都承认毕达哥拉斯定理是成立的。
但是许多证明都是一种机械化的理解:重新调整图形,瞧,这就证明了这个定理。
但是这样很清楚吗,直观地看,那就是一定是 a² b²=c² 而不是 2a² b²= c² 吗?

不是的,让我们来直观地看看。
我们要用到一个至关重要的概念:任意直角三角形都可以分解成两个相似的直角三角形。

很酷,是吧?通过一个点画一条垂线就可以把一个直角三角形分成两个小直角三角形。

几何爱好者们,试着自己证明一下这个命题:利用相似性中的角-角-角来证明。
这个示意图把一些事解释的很清楚:
面积(大)=面积(中) 面积(小)
这能说得通,对吧?
小三角形是从大三角形中切出来的,所以面积就是把较小三角形的面积相加起来。