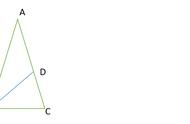
除了黄金矩形之外,黄金比例φ还有另一个可爱的几何表达,那就是它是一个边长为1的正五边形的对角线的长度。(读者可以试着用余弦定理来检验哟!)

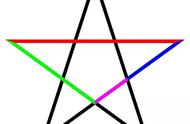
如上图所示,由对角线和底边形成的边长为1、φ、φ的等腰三角形BAD,被称为黄金三角形,它在五重对称的研究中频繁出现,例如五角星就是由五个黄金三角形构成的:

其实,定义黄金比例的方法有很多,一个非常著名的例子是斐波那契数列:

这个序列中的下一项是前两项之和,是由斐波那契提出的一种用来理解兔子种群增长的方法,它在理解人口增长方面具有重要作用。
这个数列是如何与黄金比例联系在一起的呢?最早发现这一惊人秘密的是开普勒(Johannes Kepler),他注意到,如果取这个序列中的两两相连的数字之比(后一项比前一项),得到的比值就可以形成数列: