线线平行判定定理
③线面平行→面面平行
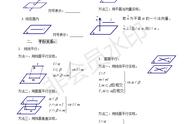
定理内容:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
符号语言:
∵a⊂α,b⊂α,a∩b=O,a//β,b//β
∴α//β
易错点:必须是两条相交的直线。

④面面平行→线面平行
定理内容:如果两个平面平行,那么其中一个平面内的任一直线都平行于另一个平面。
符号语言:
∵α//β,a⊂α
∴a//β
易错点:能推出多个线面平行,但是不能得到线线平行。

线面平行判定定理
⑤线线平行→面面平行
定理内容:一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行。
符号语言:
∵a⊂α,b⊂α,a’⊂β,b’⊂β,a//a’,b//b’,a∩b=O
∴α//β
易错点:注意只要有一组直线相交就可以。

面面平行判定定理
⑥面面平行→线线平行
定理内容:如果两个平行平面同时和第三个平面相交,那么交线平行。
符号语言:
∵α//β,α∩γ=a,β∩γ=b
∴a//b
易错点:三个平面两个交线。