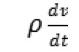四,黎曼猜测,ζ(s)的零点都位于某些地方,这个猜测就是黎曼猜想。
现在我们来解释一下。欧拉ζ函数是这样一个对所有自然数求和的级数:

需要注意的是,这个级数只在s > 1时收敛,在s ≤ 1是发散的,因此没有意义。但是黎曼提出了一种通过ζ(s)来定义ζ(1 - s)的方法,硬是把这个函数扩展到了s ≤ 1的区域。
黎曼是怎么做的呢?在s > 1的情况下,黎曼经过一番巧妙的变换,证明了下面这个等式:

这里的Γ是欧拉Gamma函数,是阶乘的扩展。如果你看不懂细节,这并不重要。真正重要的,是看右边这个关于s的表达式:把s换成1 - s,答案不变。
为什么呢?因为这时前面的分式中的分母s(s - 1)变成了(1 - s) (-s),你看,确实不变。而后面的积分当中的两个指数,-(s 1)变成了-(2 - s) = s - 2,而s - 2变成了-(s 1),你看,刚好是互换了一下,所以还是不变。结论是:右边的表达式,在s换成1 - s时,保持不变!
因此黎曼指出,左边的表达式在把s换成1 - s时,也保持不变。也就是说:

这个等式叫做黎曼的函数方程。根据这个等式,如果你知道了ζ(s),你就可以算出ζ(1 - s)。就这样,黎曼对ζ函数做出了解析延拓,从它已知的在s > 1时的值,就可以定义它在s < 1时的值!
由于时间关系,在这里我们只能讲这个证明的大略。真正惊人的是,你如果照着他的证明一路推下去,你就会看到他的结论是正确的,但他是怎么想到这个做法的?这就完全是“一剑西来,天外飞仙”!即使在专业数学家看来,黎曼的思路也非常神奇,远远不是显而易见的。