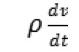因此,结果矢量的长度只与指数的实部x有关,与指数的虚部y无关;而它的方向只与y有关,与x无关。也就是说,如果给指数加上一个纯虚数,就相当于给乘方的结果做了一个旋转。如果给指数加上一个实数,就相当于改变了乘方矢量的长度,而方向不变。而如果给指数加上一个实部和虚部都不等于0的复数,乘方的结果就是既改变大小,也改变方向。
黎曼把ζ函数的自变量s从实数扩展到了复数,也就是说把ζ函数从实变函数变成了复变函数,这样做有什么好处呢?
好处在于,在某种意义上,复变函数比实变函数简单。是的,你没听错,二维的复变函数比一维的实变函数简单。
为什么呢?因为在数轴上接近一个点,只有两个方向,左和右,而在复平面上接近一个点,却有无穷多个方向,例如左边、右边、上边、下边以及任意倾斜的方向。如果对无穷多个方向做计算都能得到同一个结果,那么这是一个非常强的限制条件,能通过这样的限制条件的复变函数就很容易处理,比实变函数容易处理得多。例如,复变函数的解析延拓就比实变函数的解析延拓容易得多。因此数学界有这样的笑谈:实变函数处理的都是性质非常恶劣的函数,复变函数处理的都是性质非常良好的函数。
现在我们可以理解黎曼的做法了。用《三体》的语言说,黎曼对ζ函数发动了“降维打击”!

二向箔
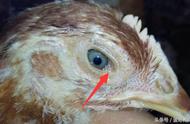
复变函数的一个特点是,许多性质是由它的零点(zero)决定的。所谓零点,就是使得这个函数取值为0的点,例如正负i就是复变函数f(z) = z2 1的两个零点。
如果你在复平面上围着一个零点做一条曲线,好比扔一个套索套住这个零点,然后求函数在这条曲线上的积分,那么你会发现积分结果完全由零点的性质决定,跟曲线的具体情况没有关系。你可以把这条曲线扩大一点或者缩小一点,拉长一点或者压扁一点,都对结果完全没有影响,你只需要知道函数在零点附近的行为就够了。
来,让我们为复变函数献上一首《套马杆》!套马的数学家,你威武雄壮!

套马杆
黎曼对ζ函数套了一通马之后,套出了下面这个惊人的等式:

这个等式说的是什么呢?左边的J(x)是一个阶梯函数,它在x = 0的地方取值为0,然后每经过一个质数(例如2、3、5)就增加1,每经过一个质数的平方(例如4、9、25)就增加1/2,每经过一个质数的三次方(例如8、27、125)就增加1/3,如此等等,每经过一个质数的n次方就增加1/n。你可以把它理解为,一个质数的n次方被算作了1/n个质数。显然,这个函数跟质数的分布密切相关。
来看等式的右边。第一项Li(x)叫做对数积分函数(logarithmic integral function),它的定义是: