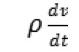“数论为我们提供了取之不尽的有趣真理——这些真理并非截然孤立,而是有着密切的内在联系,随着知识逐渐增长,我们就会不断发现它们之间新的、有时是完全意想不到的联系。”
——高斯
撰文 | 丁玖(美国南密西西比大学数学系教授)
读者,请你把一张纸卷成圆柱形,再找一支铅笔头,将它的底部紧贴在圆柱面外侧,这时笔尖朝外垂直于圆柱面。如果你保持两者垂直,将铅笔在圆柱面上绕一圈,或更一般地,让铅笔垂直于柱面,并沿其上不越过边界圆周的任意一条闭曲线移动一圈,就会发现铅笔尖的指向连续地变动,最后又回到了最初的位置。如果将铅笔头底面紧贴在纸圆柱的内面,做同样的绕圈事,结果一样。这说明这个圆柱面是“双侧”的,它具有内侧和外侧。指定了其两侧之一的定侧,就依赖“右手法则”确定了曲面上任一条闭曲线的定向——正向和反向。这是每一个孩子都能看懂的几何现象。
学过曲面积分的读者都知道,作为积分区域的曲面必须是可定侧的,否则曲面积分就无从谈起。上世纪八十年代,我在密歇根州立大学数学系的博士论文导师李天岩教授告诉我,他是这样教他读初中的儿子入门拓扑学概念的:取一张窄窄的长纸片,不是像上面那样,将两条短对边粘起来形成矮矮的圆柱面;而是先将其中一条短边扭转180度后,再与另一短边粘连。这样也得到了一个纸曲面。然后他让儿子做与上一段相同的试验,结果发现,当铅笔沿着一条方向与长对边差不多一致的闭路,保持与曲面垂直连续绕一圈后,铅笔尖终止的方向却与最初的方向恰恰相反!当然,这个现象当闭路小到只是围绕曲面上一点的圆圈时不会发生,然而导致“调转方向”反常现象发生的闭路的存在性,充分说明这个奇怪曲面有着截然不同于普通圆柱面的拓扑性质。
这个奇怪的曲面是“单侧”的,不被微积分大厦内曲面积分的房间卫士批准进门,然而它不仅形象直观,而且内涵丰富,其专业名称是“莫比乌斯带(Möbius strip)”,以发现者之一、德国数学家及天文学家莫比乌斯(August Ferdinand Möbius,1790-1868)的姓氏命名。比他早了几个月的另一个发现者是德国数学家里斯汀(Johann Benedict Listing,1808-1882)。莫比乌斯带是莫比乌斯一生中最广为人知的数学发现,因为人们一看就懂。然而,他不那么广为人知的数学工作所引出的莫比乌斯反演公式,却是本文的主题。
莫比乌斯反演
莫比乌斯反演公式最原始的思想,与我们熟知的级数部分和数列与级数通项数列的简单双边关系“心有灵犀一点通”。级数前n项的部分和是。反过来,级数的第n项可写成a=s-s(约定s=0)。如果定义一个特殊的数列{μ}:μ=1,μ=-1,且当n≥2时,μ=0。那么上述部分和与通项的“相互表出”就是当且仅当。
莫比乌斯反演公式至今有许多推广和变种,但最有名也最简单的那个堪称“经典”,在数论和组合数学中有众多用途。为了理解这个原始公式,需要介绍几个初等术语。首先,所谓的“反演(inversion)”是中学代数里反函数概念的推广。当函数y=f(x)在定义域上将不同的自变量值x映成不同的函数值时,该函数f引出了对应的反函数f,它把f的函数值y映回到导致该值的自变量值:x=f(y)。这样,函数定义域中的所有x和值域中的所有y建立了一对“反演关系”:y=f(x)当且仅当x=f(y)。作为例子,函数y=x的反函数是x=y。虽然函数有反函数,但我们写不出它的代数表达式。初等数学里可逆函数及反函数的反演表示可以推广到更高等、更抽象的数学。
比如,将定义在全体自然数上的所有数列全体记成X,设想有个对应关系T将X中的每个数列{x}映成一个数列{y},这个变换一般称为“算子”,尤其在泛函分析学科。如果T将不同的数列映到不同的数列,那么就有逆算子T,它把T的值域中的每个数列映回到其来源数列,即{y}=T{x}当且仅当{x}=T{y}。这也给出了一个反演关系。
现在,可以叙述数论中经典的莫比乌斯反演公式了。设f为一“算术函数”,即它的定义域是所有自然数之集,函数值为复数。自然,算术函数可与它在所有自然数上的值构成的数列等同起来。在数论中,如果自然数d是自然数n的一个因数,即n=dq,其中q也是自然数,则这个关系写成d|n。对所有的自然数n,下式

定义了一个新的算术函数g。那么将f映到g的算子T有逆算子,其表达式即为所谓的莫比乌斯反演公式

其中μ定义在上,称之为“莫比乌斯函数”:μ(1)=1;若n是k个相异素数之积,则μ(n)=(-1);若n的素数分解式包含一个素数平方,则μ(n)=0。
历史上,莫比乌斯反演公式的源头是莱比锡大学莫比乌斯教授于1832年发表的一篇德语论文,英文翻译为(《一种特殊类型的级数反演》)。但文中研究的“反演问题”与上面的(*)和(I)无关,而是在级数变换的反演级数变换F(x)=中,寻求系数数列{b}与原系数数列{a}之间的关系。不过,他在这篇留名数学史的文章中给出了后人命名的莫比乌斯函数μ表达式及其因数和公式。
莫比乌斯函数
鉴于莫比乌斯函数μ在反演公式中所起的关键作用,我们来探讨它的基本性质。先熟悉一下莫比乌斯函数值数列中的最前面一打数字:μ(1)=1,μ(2)=-1, μ(3)=-1,μ(4)=0, μ(5)=-1, μ(6)=1, μ(7)=-1, μ(8)=0, μ(9)=0, μ(10)=1, μ(11)=-1, μ(12)=0。该函数的第一个基本性质为:它是积性(multiplicative)的,即只要两个自然数m和n互素(除1外没有其他正公因数),等式μ(mn)=μ(m)μ(n)就成立。事实上,当mn=1时,m=n=1,故μ(mn)=1=μ(m)μ(n)。若mn>1,先设m=p…p和n=q…q,其中p,…,p以及q,…,q为相异的素数,则μ(mn)=(-1)=(-1)(-1)=μ(m)μ(n)。上式当m=1或n=1时也成立(注意1不是素数)。现设m和n中至少一个以素数平方为一因数,那么此素数平方也是mn的因数,故μ(mn)=0=μ(m)μ(n)。以上是直接的证明,作为练习,读者也可以用数学归纳法给出第二个证明,这是训练大脑的好机会。由0=μ(4)≠(-1)(-1)=μ(2)μ(2)知,莫比乌斯函数不是“完全积性的(completely multiplicative)”,即等式μ(mn)=μ(m)μ(n)并不总是成立。
由定义知μ(1)=1。下面我们证明一个非常管用的等式:对任何大于1的自然数n,