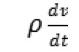狄利克雷卷积
学过傅里叶变换的读者对函数之间的卷积(convolution)运算不会感到陌生。两个函数f和g的卷积f*g被定义为其中一个函数与经过反射与移位作用后的另一个函数乘积的积分,表示一个函数的形状如何被另一个函数改变。如果f和g的定义域都是整个实数轴,那么它们的卷积是。运用积分的变量替换法,易证f*g=g*f,即卷积运算满足交换律。傅里叶分析中的卷积定理说,如果F和G分别是f和g的傅里叶变换,那么F和G的乘积的傅里叶逆变换是f和g的卷积。对于工程数学中常用的拉普拉斯变换,也有类似的卷积定理。
那么,卷积的思想和方法和“莫比乌斯反演”也有关系吗?当然有!这就是在数论中用于算术函数的狄利克雷卷积,此概念简直就是莫比乌斯反演的直接推广。它的定义与莫比乌斯反演公式(I)右端的表达式极为相似,除了那里的莫比乌斯函数μ被一般函数取而代之:令f和g为算术函数,则f与g的狄利克雷卷积是算术函数

显见狄利克雷卷积也像整数相乘那样是可交换的。此外,在函数加法和内涵为狄利克雷卷积的“乘法”下,所有算术函数的全体也像所有整数全体那样构成一个可交换环,称为狄利克雷环。整数环的乘法单位元是正整数1,而狄利克雷环的乘法单位元就是前面提到过的算术函数ε,其官方名字是“恒等算术函数(identity arithmetic function)”,并且有恒等式。自然,它不是巧合。事实上,用上面证明莫比乌斯反演公式一样的途径,就能很快验证f*ε=ε*f=f。
此外,狄利克雷卷积也像整数乘法一样,满足结合律和分配律:(f*g)*h=f*(g*h)及f*(g h)=f*g f*h。就狄利克雷环而言,当且仅当算术函数f满足f(1)≠0,它有狄利克雷逆,即存在算术函数f使得f*f=ε。特别地,常数函数1的狄利克雷逆就是莫比乌斯函数μ,即有下一段论证中所需要的关系1*μ=ε。这里我们已用1代表在自然数集合上取值处处为1的函数,它的名称是“单位算术函数(unit arithmetic function)”。
有了卷积的强大工具,我们可以给莫比乌斯反演公式一个更简洁的证明。首先,公式(*)可写成卷积形式g=f*1。进而,反演公式(I)从右到左的推导过程是

反过来,在(I)成立的条件下,如下步骤推导出(*)为真:

由此可见,在狄利克雷卷积的语境内,经典莫比乌斯变换的表述就是:
g=f*1当且仅当f=g*μ。
一般理工科大学生大概是从傅里叶级数或偏微分方程边值问题中得知德国数学家狄利克雷(Gustav Lejeune Dirichlet,1805-1859)的大名,但不要误以为他只专“分析数学”,就像今日几乎所有数学家那样只精通一门手艺。他同时是数论大家,开创了解析数论分支。函数的现代定义也源自于他,让今日全球的中学生从这最合理的定义中获益。
既然莫比乌斯反演只是“单位算术函数1的狄利克雷逆是莫比乌斯函数μ”这个事实的“代名词”,原始的莫比乌斯变换双公式(*)和(I)马上可以推广成如下的一般反演公式:假定算术函数α有狄利克雷逆,那么