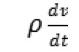。 (1)
例如,当n=20=2·2·5,它的正因数为1, 2, 4, 5, 10, 20,故有

上面的例子隐藏着等式(1)的证明思路。根据算术基本定理,令为n的素数分解,则由于当n的因数d是平方数倍数时μ(d)=0,等式(1)左边的和式中只需考察d为p,p,…,p中某些相异数的积,以及d=1。这些d为:1=C(k, 0)个1,C(k, 1)个p,C(k, 2)个pp, …,C(k, k)=1个pp…p,其中C(k, i)=k!/[i!(k-i)!]为从k个物体中每次选取i个形成一组的所有组的个数。故由二项式定理,

现在我们着手证明莫比乌斯反演公式(I)。首先,根据算术函数g的定义并交换求和的次序(道理等同于将一组有限个数分别按两种方式分成若干小组,按各自方式先加组内数再把和数相加的最后总和一样。最简单的情形是:一组排成长方阵的数相加,无论一行一行地加还是一列一列地加,结果一样,即),(I)的右端

当c=n时,,而当1≤c<n时,由(1)式知。从而我们得到等式