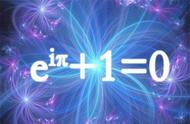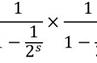1/n表示在我们的周期内赚到的利润。我们假设利润是实的——但是如果它是虚的呢?

现在我们的利润被推向了90度方向,但是这不影响我们的长度。(这是一个比较难理解的概念,因为这就像我们在一个比较长的斜边下构造一个三角形。我们在处理一个极限;斜边有一个在我们误差范围内难以发现的增加。我们需要微积分来帮我们弄清楚,但是这个还是改日再谈吧)。

我们每次把 i 单位的增长应用到无穷小量上。每一次应用都是轻轻把它推向90度方向。没有所谓的“越来越快”的旋转,因为它与增长方向始终保持垂直,它只是推向一个新的方向而已( 1角度而已)。 所以我们发现了另一种表示圆的方法!
圆周运动:始终沿着90度的方向进行旋转(虚增长率)
那么,欧拉公示就是在说“指数的虚增长最后就是一个圆的轨迹”。而这个轨迹跟用正余弦函数表示的虚数画出来的轨迹一样。在这里用“指数”可能有些不恰当,因为我们沿着一个圆始终做着匀速运动(最好还是称为“连续改变”)。但是我们现在主要面对的是增长就是一个复合的,累积的增长。
11.6 一些例子你现在可能不相信我。以下是一些帮助你直观化思考的示例。
示例:e^i
也就是 e^(i.1) , 即 x=1 的情况. 直观的来看,不需要用计算器我们就知道这是在说“沿着单位圆前进1弧度”:
e^i =cos(1) isin(1)=0.5403 0.8415i
结果不是一个简洁的数字,但对计算器而言没有问题。输入这些的时候记得把你的计算器调到弧度模式。
示例:3^i
这就需要一些技巧了——这不是我们通常见到的形式。但是记住,

——真正的问题就是“我们怎么把1做变换”呢? 我们希望有一个最后增长率为3倍或者说即时增长率为ln(3)的增长,但是,下面变形利用 e 变成了: