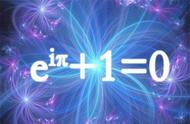我们得到了一个负旋转!我们每单位时间将要以 π/2 的速度进行旋转。转多长时间呢?其中暗示了1个单位时间;一个单位时间的旋转就是-i:
i^i =0.2078……
(i^i)=-i
而且,看看整个过程,如果我们给它平方一下的话:
((i^i)^i )2 =-1
这就好比是两倍的旋转:2是一个实数,所以它让我们的旋转翻倍到-180度。或者也可说它做了两次-90度的旋转。 最后得瑟一下,它们确实都是些奇怪的指数,但是通过类比我们可以很轻松的把它们搞定。

我们可以既有实数增长也有虚数增长:实数增长改变大小,虚数增长进行旋转:

一个复数增长率(a bi)就是混合了实数增长与虚数增长。实数部分就表示“每秒增长100%”而虚数增长就是“旋转b秒”。记住,虚数并不能把不同的方向进行复合,所以它只是线性相加。 根据这个想法,我们可以把任何点用不同大小的圆(a bi)表示出来!半径就是ea 而角度由eib 决定。这就像把数字放到“创世界”中两次:一次你让它的大小发生变化(一秒),另一次就是让它的角度旋转(b秒)。或者你可以先旋转再增长! 我们想知道得到6 8i的最终倍数所需要的增长数。这就是在问一个复数的自然对数:我们如何把e变为6 8i?
半径:我们需要一个多大的圆?大小是√(6² 8²)=10.这就意味着需要花ln(10)=2.3秒的时间来达到这个数值
旋转的角度:那个点的角度是多少?我们可以使用反三角函数来计算:arc tan(8/6)=53度=0.93弧度。
组合结果:ln(6 8i)=2.3 0.93i
11.8 为什么真很有用?最起码的,欧拉公式给了我们一个另一种方法来描述沿着圆的运动。当然我们也可以用正余弦函数来表示——为什么如此特别呢? 这只是角度不同而已。正余弦函数运动就是在水平坐标和垂直坐标中运动的点而已。

欧拉公式使用极坐标——你的角度与距离多少?再一次的,这是两种描述运动的方法而已:
笛卡尔坐标:向东3个单位,向北4个单位
极坐标:在71.56角度方向上移动5个单位
这取决于是哪种问题,才能那个决定极坐标还是笛卡尔坐标哪个更有用。欧拉公式可以让我随意的进行转换。同样的 eix 转化为正余弦函数,我们可欧拉公式被认为是数学中最优雅的公示之一——而且确实可以理解其中的奥妙。(完)