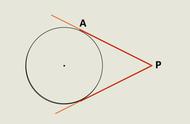
他给出的定义非常简单:切线就是曲线上的割线在两个交点无限接近时所对应的那条直线。

如上图所示,红色线是一条割线,它与曲线交于两点。让其中一个交点固定不动,而让另一个交点沿着曲线不断靠近那个不动点,在这个过程中,割线不断旋转。
当二者之间的距离无限靠近时,它们决定的那条割线不再动了,这就形成了一条特殊的割线——哦,此时不再是割线了,而是一条被定义为“切线”的直线。
所以,切线是什么?切线就是割线的交点无限靠近时的极限。它的斜率可以通过极限运算确定,即
根据导数的概念可知,这个极限正好就是函数在该处的导数,即 据此,我们可以给切线一个非常严格的数学定义。那就是:
设有曲线 ,其导数为 。若直线过点 ,且具有斜率 ,则称直线为曲线在点 处的切线。
根据这个定义,只要知道曲线的函数表达式,就可以通过求导的方法得到曲线在任一点的切线的斜率,加上这个已知点,我们就能唯一的将切线确定下来。
当然,对于非光滑的曲线,由于在某些位置,导数是不存在的,因此切线也就不存在了。
莱布尼兹关于切线的定义里,蕴含了他的微分思想。
学过微分的都知道,微分是无限趋近于零,但却不等于零的值。这保证了两个点还是两个点,只是彼此无限靠近!这一点非常重要。
因此,切线是曲线上无限接近,但又没有完全重合的两点决定的一条直线。
这个定义与大多数人心目种的切线定义不同,很多人往往认为切点是一个点,其实你想想,一个点怎么能确定一条直线呢?必须要两个点啊!
所以,切点从本质上讲包含两个点,两个无限靠近的点。
呃,是不是有点被颠覆世界观的的感觉?切点不就是一个点嘛,怎么会是两个点?
是的,如果你只是关心位置,那么切点就是一个点,它就是那个不动的点蜕变而来的。但只是在那个动点无限靠近时,它才转正成为切点!在此之前,它不是切点。
所以,莱布尼兹的定义是多么美妙!
而莱布尼兹的定义与阿波罗尼奥斯的定义是一致的,下面动画清楚的显示这一点:你无法在切线与曲线形成的角里再插入一条直线。

最后再来看一个问题:曲线上任一点是否只有一条切线呢?
很多人的答案是肯定的,并且在学习电场时,还据此来理解电场线为什么不能相交的问题。但恐怕很多人在这个问题上有点逻辑颠倒。实际上,电场线不能相交,那是因为任一点场矢量的方向是唯一确定的,并不能说明曲线上每点只能有一条切线!
实际上,过一点有多条切线的情况是存在的!
比如下面这种被称Pascal或limaçon的曲线,在原点处就有两条切线。这是一种奇点的特殊情况,这种情况下,前面的定义失效了。但可以根据纯代数方法找到这些奇点的切线方程,这里就不涉及了。

与曲线的切线类似,与给定点处的曲面相切的平面是“刚好接触”该点处曲面的平面。例如,下图中,球面与平面刚好接触,平面是球面的切面。