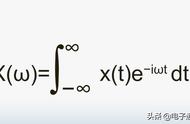虽然说他是一位科学家和数学家,然而傅里叶对于热学太过于痴迷了,封建迷信害死人啊, 他认为热能包治百病,于是在一个夏天,他关上了家中的门窗,穿上厚厚的衣服,坐在火炉边,于是他被活活热死了。
从这个例子里我们发现,即使是大科学家大数学家也很容易迷信谣言、伪科学,掉坑里呀!

傅里叶墓碑
而虽然傅里叶变换是诞生于热学,但是到了计算机时代,人们发现,这个公式可以用来表示分析信号的成分,也可用这些成分合成信号。一下子,傅里叶变换的重要性就立马凸显了起来。
那么我们就正式开始切入正题,我们这里只是简单了解一下傅里叶变换的基础定义与内容,不涉及傅里叶级数、离散时间傅里叶变换之类的。
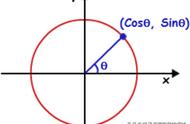
首先知识点先排除,什么是正余弦波,首先,直角三角形中,∠C=90°;任意一锐角∠A的对边与斜边的比叫做∠A的正弦,也就是sinA=a/c。∠A的余弦是它的邻边比三角形的斜边,所以co sA=b/c。

那么正线函数和余弦函数在平面直角坐标系的呈现就是这样:

这样的知识点对于 8 岁小孩子来说,还是可以简单理解成功的。所以说正余弦波就是指正坐标轴余弦函数的波形。
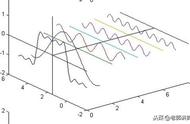
正题来了,傅立叶变换(的三角函数形式)的基本原理是:多个正余弦波叠加(蓝色)可以用来近似任何一个原始的周期函数(红色)