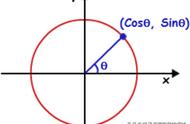
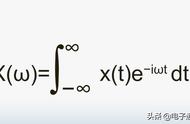而频域呢,就是描述信号在频率方面特性时用到的一种坐标系,频域就是装着正弦函数的空间,自然而然的,正余弦波是频域中唯一存在的波形。

心电图符号
我们从时域我们可以观察到心脏随着时间变化在不停地跳动的情形,但是从频域来看,就是一个简单的心电图符号。如果时域是运动永不停止的,那么频域就是静止的。
在很多领域我们都可以用到时域和频域,在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。

刚刚我们讲了多个正余弦波叠加可以用来近似任何一个原始的周期函数,我们心脏不同时间、不同强度的跳动就成了我们所看到的心电图。就可以看作正余弦波叠加成的周期函数。同样的,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲,也可以看作余弦波叠加成的周期函数。

而对于信号来说,信号强度随时间的变化规律就是时域特性,信号是由哪些单一频率的信号合成的就是频域特性傅里叶变换实质涉及的是频域函数和时域函数的转换。
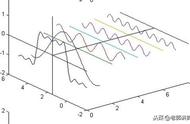
那么正余弦波是如何叠加成周期函数的呢?随着正弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,不仅仅是矩形,你能想到的任何波形都是可以如此方法用正余弦波叠加起来的。