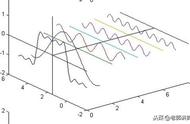
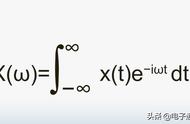各位看到了那一条条正余弦波了吗?时域是永远随着时间的变化而变化的,而频域就是装着装着正余弦波的空间。

从这个方向看过去的侧面图就是频域
从时域来看,我们会看到一个近似为矩形的波,而我们知道这个矩形的波可以被差分为一些正弦波的叠加。而从频域方向来看,我们就看到了每一个正余弦波的幅值,每两个正弦波之间都还有一条直线,那并不是分割线,而是振幅为 0 的正弦波!也就是说,为了组成特殊的曲线,有些正弦波成分是不需要的。
随着叠加的递增,所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个正弦波叠加起来才能形成一个标准 90 度角的矩形波呢?不幸的告诉大家,答案是无穷多个。
所以,我们可以再来看一下开头的动图,是不是就更加能够理解了。

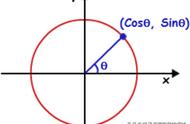
而想要完美地表示正余弦波,除了正余弦波的幅值是不行的,还需要相位谱的帮忙,什么是相位呢?就是对于一个波,特定的时刻在它循环中的位置:一种它是否在波峰、波谷或它们之间的某点的标度。
不同相位决定了波的位置,所以对于频域分析,仅仅有幅值是不够的,我们还需要一个相位谱。频谱的重点是侧面看,相位谱的重点则是从下面看。

如上图所示:投影点我们用粉色点来表示,红色的点表示离正弦函数频率轴最近的一个峰值,而相位差就是粉色点和红色点水平距离除以周期。将相位差画到一个坐标轴上就形成了相位谱。
总结一下,傅立叶变换就是多个正余弦波叠加可以用来近似任何一个原始的周期函数,它实质是是频域函数和时域函数的转换。而其中时域就是永远随着时间的变化而变化的,而频域就是装着装着正余弦波的空间,代表着每一条正余弦波的幅值,而表示正余弦波除了幅值是不够的,就还有相位谱。