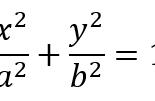二次函数的三种表达式:
知识总结
二次函数的表达式有三种:
一般式 y=ax2 bx c(a≠0);
顶点式 y=a(x-h)2 k;
交点式 y=a(x-x1)(x-x2).
三种表达式各有特点,下面我们分别细说。
一、一般式:
一般式的表达式是y=ax2 bx c(a≠0),a、b、c分别是二次项、一次项、常数项的系数,a、b、c分别有什么用途呢?
1、a的符号确定了抛物线的开口方向,a>0时,抛物线的开口向上,a<0时,抛物线的开口向下.
2、因为对称轴为直线,如果a、b同号,<0,则对称轴在y轴右侧;如果a、b异号,>0,则对称轴在y轴左侧,因此根据a,b的符号可以判断出对称轴的位置:左同右异(即:a、b同号,对称轴下y轴左侧,a、b异号,对称轴在y轴右侧).
3、因为抛物线与y轴交点坐标为(0,c),所以根据c的符号可以判断抛物线与y轴交点的位置:当c>0时,交点在y轴正半轴,当c<0时,交点在y轴负半轴,当c=0时,抛物线经过原点(0,0).