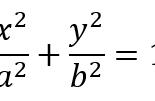任何两个函数图像的交点都可以联立两个函数的解析式,通过解方程组求出交点的坐标.
比如,求抛物线y=ax2 bx c(a≠0)与x轴的交点情况,因为x轴的解析式是y=0,所以联立两个解析式,解方程组就可以得到交点坐标.联立 解方程组即可,抛物线与x轴交点的情况其实就是方程ax2 bx c=0解的情况:
(1)当△>0时,一元二次方程ax2 bx c=0有两个不相等的实数根x1,x2,方程组有两组解,那么抛物线与x轴有两个交点,坐标分别为A(x1,0)、B(x2,0).反之也成立.
(2)当△=0时,一元二次方程ax2 bx c=0有两个相等的实数根x1=x2,方程组有两组相同的解,抛物线与x轴有一个交点,这时,二次三项式ax2 bx c是一个完全平方式,抛物线与x轴的这个交点就是抛物线的顶点.反过来,如果抛物线的顶点在x轴上或者抛物线与x轴有一个交点,那么一元二次方程ax2 bx c=0有两个相等的实数根,二次三项式ax2 bx c是一个完全平方式.
总结:△=0、一元二次方程ax2 bx c=0有两个相等的实数根、二次三项式ax2 bx c是一个完全平方式、抛物线的顶点在x轴上、抛物线与x轴有一个交点都是同一个意思.
(3)当△小于0时,一元二次方程ax2 bx c=0没有实数根,方程组无解,抛物线与x轴没有交点.
推广:求抛物线y=ax2 bx c(a≠0)与直线y=kx b(k≠0)的交点坐标,只需联立两个解析式,解方程组即可.一元二次方程ax2 bx c=kx b的解的情况就是两个函数图形交点的情况,可以类比抛物线与x轴交点情况.其实任意两个函数的交点都可以联立两个函数的解析式解方程组求解.
经典例题:
已知抛物线与x轴交于A(1,0),B(-4,0)两点,与Y轴交于点C,且AB=BC,求此抛物线对应的函数表达式。

‘