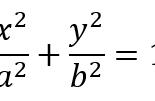这里面我们需要有一个思维的转化,当涉及动点在直线运动且有速度时候,我们可以设成含有“t”的线段,而且这样线段其实我们就可以视为“固定线段”,根据已知条件找到这样线段的数量关系建立方程,求出方程的解。这一类动点问题,我们就可以视为“固定线段”。
具体步骤

第二小问解析
通过读题,我们发现这个内容,点G固定在AB直线上,这个时候很多学生思考的问题是:点E和点C运动到什么时候,点G才能在AB上。很多学生都是利用这样思维模式去思考题,只要涉及到动点问题加上动点运动位置问题,就会顺着题去思考,然后就走入一个漩涡里面出不来。
这一类题,一定要跳出来这样一个怪圈,那么如何思考呢?
我们可以通过已知条件结合前一问证明内容进行思考,已知条件能够给我们提供什么内容。进而解决问题。那么我们来看看都给我们什么已知条件了和如何结合上一小问解决问题

已知条件 上一小问分析结果:CE为三角形BOA中位线
这题是求线段长,所以我们可以先通过几何看看是否可以求出线段长,如果不能,我们可以利用“方程思维”进行解决问题。
具体步骤

第三问解析
通过读题,这问涉及到的问题是等腰三角形存在性问题,所以我们需要做的内容就是先看看这个等腰三角形顶点几定几动。