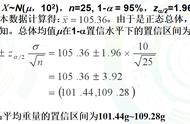当代,数学是理解世界的方式,也是科学的基础。
重大的科技进展无不与数字息息相关;没有数学就没有现在的“手机、电脑、人工智能、云计算”,我认为四种理科概率可以加入日常学习进度中,它对你的未来会有所帮助。
拥有数理逻辑思维,它能让自身清晰的算出做每件事成功的概率有多少?也可以在大脑中提前建立“认知框架”;最先需要认识的是“贝叶斯定理”。
它是什么呢?
由英国数学家贝叶斯( ( Thomas Bayes 1702-1761 ) 提出,主要用来描述两个条件之间的关系,先熟悉下它的公式:P(A|B)=P(B|A).P(A)/P(B)。
我知道你一看公式就难受,但是蕴含了巨大能量。
它能做什么呢?主要指在信息和条件有限的情况下,基于过去的数据,通过动态调整的方法帮助我们一步一步测算出事件发生的真实概率。
我尽量用文科思维进行表述,它包含四个方面:1)先验概率,2)条件概率,3)全概率。
方便理解,随便举两个例子:
1)我最近10天有2次迟到,请问我今天迟到的概率有多少?很显然,迟到事件发生的概率是2/10,也就是P(迟到)=1/5=20%,这就叫做先验概率。
2)今天早上堵车,今天我迟到的概率是多少?注意这里已经不同上述,“迟到”是一种事实结果,而造成迟到的原因可能是堵车。
那么堵车就是影响结果的条件,这种情况下就属于“条件概率”,即P(A|B);公式也比较简单,即P(A|B)=P(AB)/P(B)。
比如我近10天遭遇5次堵车,其中两次迟到,那么今天早上如果又堵车了,我迟到的概率就是40%,用公式计算是:P(迟到|堵车)=P(堵车且迟到)/P(堵车)=0.2/0.5

一般情况下,条件概率中的条件都是我们已知的,现实中经常出现在“受到什么相关的事件影响,我们......”。
如:雷军在创业之处用2年半的时间,把手机从零做到中国出货第一,全球第三;然而在2016年时全球出货量跌出TOP5,当时有评论说“世界上没有任何一家业绩下滑的公司能够成功逆袭”。
经过战略调整,2017年第二季度小米走出低估重回前五,在企业家论坛某次采访中雷军做了一些分享,他说:
过去一直专注线上而错过线下换机潮,而高性价比是效率革命,当时专注电商,天大陷阱就在于“电商占比零售总额的10%”。
小米就算线上市场100%是自己的,可在整个市场依然是10%,意识到这点才建立零售店铺,重整旗鼓。
这里的事情A(手机销量)与事情B(电商之占商品零售额10%)就是相关事件,那条件概率逻辑上可以给我们什么启发呢?
当根据数理思考时,我们必须留意什么是“给定”的,或者位于所讨论的条件概率中动态方面究竟要被理解成什么。
由因及果就是先验条件概率,也就是知道原因,求结果的概率;跟先验概率相反,我们由结果推导出原因的概率叫做“后验概率”。
也就是,依据“结果信息”所计算出原因发生的概率,它是贝叶斯定理重要的基础。
比如:我中午拉肚子啦,是因为昨天吃火锅的概率有多大?;我们公司虽然业务今年下滑,除市场竞争外,可能是高管团队人不行;这种概率可以用来做原因推理。
很多人会有疑问,我们求后验概率和先验概率的意义是什么?因为传统频率是无法解决实际问题,实际问题中一般由多个条件组成的复杂条件,那什么是复杂条件呢?
比如,拉肚子这件事,昨天吃火锅后晚上还喝了几杯凉水,睡觉时还喝了牛奶,这是复杂的事件对不对?
如果我们知道引起拉肚子的所有事件,且这些事件都是相互独立且互斥的,那么想求出拉肚子的概率,就可以将整个复杂时间拆分出几个条件概率,这就是全概率。
关于如何计算这里不做详细追溯,相信你也会看的头疼。
这就是贝叶斯公式推倒的过程,核心思想是“当你不能准确一个事物的本质时,你可以依靠与事物特定相关的时间出现的多少,频率去判断其本质属性的概率。
这个角度出发,可以得到什么启发呢?
贝叶斯概率用在各种场景中,任何大事件形成的概率都是由各种“小事件”组成的,而事件代表信息,信息出现频率和准确度直接影响到“先验概率和后验概率”。
就像公司做一场营销活动,当分析渠道拉新效果时,我们不能只针对结果做假设,还要思考前提条件;这个前提条件的忽略可能最终影响自身对整个事情的判断。
可见,数理逻辑和哲学逻辑相似,都讲究“大前提”和“条件数”“准确率”三方面,那么概率大就同等于“概率权”多吗?其实未必;前者表述现在状态,后者在推演未来。
要知道,我们所了解的每个概念都需要用在某个具体领域,这样才能核算出概率权,因此有必要了解一个概念,“局部和整体的关系”。

一个人和平台是种关系、一个人和公司是种关系、甚至公司和平台也是某种链接关系;但在这些关系中我们发现很难抓住“有效变量”。
换句话说:“努力看不到尽头”不是努力的问题,而是没有把它精细化,搞懂规则,因此想要形成关键变量离不开四个因素:1)领域,2)团体,3)分布定律,4)发展状态
四者打包称之为“局部”,即我所在什么领域,它有多大规模、覆盖情况和发展是什么样、行业整体分布状态如何。
和它所对应的是整体,位于主导地位统率着部分甚至影响到部分性能状态的变化。举个例子:
在微信APP中平均分配多个版块对不对,如公众号、社群、通讯录、朋友圈等;看似无连接的功能基于用户量就会出现自组织涌现的状态。
如果你知道公众号总注册数量和自己所在行业数量,那么就可以清晰的计算出是否值得投入这门生意;或者分析完垂直领域内的内容营销方式就可以进行“创新”对不对?但这仅代表“局部”;按照统计学来说,一个行业的分布状态有:1)幂律分布,2)泊松分布,3)正态分布
第一方面:幂律分布指行业整体中,极少的关键公司带来绝大多数的收益,其他大多数普通事物只能获取少量收益;平时经常说的马太效应,长尾理论,帕累托法则和此意思相似。
就像短视频平台的网红,只有极少数能够做到百万粉丝收入过亿,收入不超过五位数的却有几千万。
它能说明什么呢?行业中永远都有二八定律,如果想跑到前面,就要思考别人没有做过的领域或者“创新别人的事情”,千万不要与大玩家进行重合。
这如同元气森林在气泡水市场打开新天地,实则是找到“巨头痛点”,进行创新加上团队效率的结果才起到“关键变量”。

第二方面:泊松分布是法国数学家西莫恩·德尼·泊松 (1781–1840) 于1837年提出,在实际生活领域有非常广泛的应用;主要描述在某个时段或空间内随机发生随机事件次数的概率。
简而概之,可以根据过去某个随机事件在某段时间或者“空间”内发生的平均次数,预测随机事件在未来同样长的“时间、空间”内发生K次的概率。
例如,某家医院在一定时间内到达的人数,超市收银台在某段时间内结账的人数等。它告诉我们“留足冗余”和“效率平衡”的重要性;比如参加参加一次会议,平均路上是30分钟,这次最好准备45分钟以保证不会堵车也能赶到。
换句话说,冗余之后在整体中风险会显著降低,凡事留后路就是这意思。
第三方面:它也叫“常态分布”,基本上能描述所有常见的事物和现象,比如正常人群的身高、体重、考试成绩、家庭收入等等,这里的描述是什么意思呢?就是说,这些指标背后的数据在整体中都会呈现一种“中间密集”,量变稀疏的特征。
以身高为例,服从正态分布意味着大多数人的身高都会在人群的平均身高上下波动,特别矮或特别高很少见。了解其基本思想后,我们需要掌握什么要点呢?
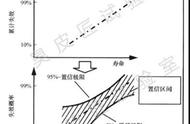
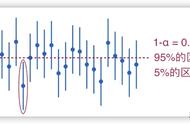
正态分布是“连续型随机变量分布”的一类,对于连续随机变量,我们不要关注“点概率”,而是要关注“区间概率”。这如同饮料新品投放市场测试,10个人说不好喝不重要,重要的是看“海淀区”整个区域的分值。
通过这三种概率,我们可以得到什么?在一个整体行业市场中,自身所从事的领域和团队代表“局部”,想要关键变量指数增长就要洞察行业分布状态。
追头部没有机会,那就在“正态”分布当中做创新;同时注重泊松分布,凡事给自身留后路,以便错过机会进行加速调头。
总而言之,整体是局部整合后的认知,我们也可以用理科概率中的“后验概率”来推导每一步的计划是否可行,足以建立高壁垒。
好了,说这么多;基于此之上我们来总结下如何提高“概率权”,(基于现在的计算,对未来的选择权)?做好这些,可以解决个人70%关于发展的问题,甚至它可以让你源源不断增长。