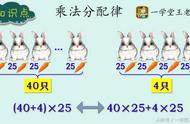
(2) 赋予算式图形情景。
如:借助场地扩建问题,求扩建后场地面积这一类题(如下图)。把算式与图形结合起来,渗透数形结合思想,帮助学生理解乘法分配律的含义。

(3) 赋予算式模型意义。
如:计算81×99 81这一类题,可以先让学生思考算式是由哪两部分组成;再思考把算式理解成81个99和1个81相加,还是理解成99个81和1个81相加,让学生在比较中获得正确的算式意义;最后在算式中去添加1使之变成81×99 81×1,将学生不熟悉的算式纳入到已具备的乘法分配律结构之中,使之与原来熟悉的数学模型结构相吻合。

3. 借助模型,强化记忆。
把乘法分配律的内容识记为爸爸和妈妈都爱我等于爸爸爱我加妈妈爱我,强化学生对乘法分配律模型结构的记忆,为枯燥的学习平添几分乐趣。

五、查漏补缺
根据以上对策,我们调整了教学预案,有针对性地进行查漏补缺。随后,专门针对学生的易错点编写了测试题对全年级近四百名学生进行摸查,统计出各题的正确率,并进一步分析学生对乘法分配律的掌握情况。