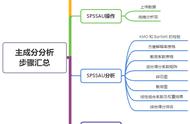
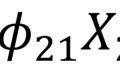一个例子主成分分析(principal components analysis,简称PCA)是一种降维分析,将多个指标转换为少数几个综合指标,由霍特林于1933年首先提出。
主成分分析方法之所以能够降维,本质是因为原始变量之间存在着较强的相关性,如果原始变量之间的相关性较弱,则主成分分析不能起到很好的降维效果,所以进行主成分分析前最好先进行相关性分析。
中心城市的综合发展是带动周边地区经济发展的重要动力。因而,分析评价全国35个中心城市的综合发展水平,无论是对城市自身的发展,还是对周边地区的进步,都具有十分重要的意义。
原始数据及指标解释。我们选取了反映城市综合发展水平的12个指标,其中包括8个社会经济指标,分别为:—非农业人口数(万人);—工业总产值(万元);—货运总量(万吨);—批发零售住宿餐饮业从业人数(万人);—地方政府预算内收入(万元);—城乡居民年底储蓄余额(万元);—在岗职工人数(万人);—在岗职工工资总额(万元)。
4个城市公共设施水平的指标:—人均居住面积(平方米);—每万人拥有公共汽车数(辆);—人均拥有铺装道路面积(平方米);—人均公共绿地面积(平方米)。
问题:请使用主成分分析,将这12个指标综合为少出几个综合指标。

在开始解决这个问题之前,有必要先了解一下主成分分析的基本原理及其求解方法。
主成分分析基本原理1、几何意义
如下图所示,平面上散落着N个点,无论是沿x1轴方向,还是沿x2轴方向,均有较大的离散性,即这些点所代表的信息由两个指标x1,x2所决定,若只考虑x1和x2中的任何一个,原始数据中的信息均会有较大的损失。

如果我们将坐标轴进行一个旋转操作,得到新的坐标轴y1和y2,如上图所示。则会发现这些点只在y1方向上有较大的离散性,即y1可以代表原始数据的绝大部分信息。
也就说原来需要2个指标才能表示的信息,经过一些处理后,变成只需要1个指标,而且不会损失太多的信息,即所谓的降维。
上述坐标旋转公式如下:

从公式可以看出,坐标旋转本质上是线性变换,将原来的x1和x2,通过线性变换转换为y1和y2。
所以主成分分析其实就是将原来的指标进行线性变换,生成新的指标,下面介绍主成分分析更一般的数学模型。
以下提到的数学理论,不感兴趣可以略过,因为主成分分析一般都是通过工具(如SPSS)进行,不需要手动计算!
2、数学模型
主成分分析数学上的处理是将原始的p个变量作线性组合,作为新的变量。