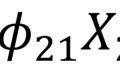总方差解释反映了各个主成分的贡献率及累计贡献率,第三列表示贡献率,第四列表示累计贡献率,可以看到,提取前3个主成分,累计贡献率就可以达到87%以上,即这3个主成分集中了12个原始变量的87%的信息。
(4)成分矩阵(或因子载荷矩阵)

成分矩阵(或因子载荷矩阵)反映了提取的3个主成分与原始变量的相关性,从上面可以得出以下结论:
- 主成分1跟原始变量x1,x2,x3,...,x8的相关性较强;
- 主成分2跟原始变量x10,x11,x12的相关性较强;
- 主成分3跟原始变量x9的相关性较强。
对主成分进行解释:
- 原始变量x1,x2,x3,...,x8反应的是城市规模和经济发展水平,所以主成分1命名为城市规模及经济水平;
- 原始变量x10,x11,x12反应的是城市基础设施,所以主成分2命名为城市基础设施;
- 原始变量x9反应的是城市人均居住面积,所以主成分3命名为城市人均居住面积。
综上,通过主成分分析,将反应原始数据的12个指标综合为3个综合指标,分别为:
- 城市规模及经济水平
- 城市基础设施
- 城市人均居住面积
从而起到了降维的作用。
你是否使用过主成分分析(PCA)呢?欢迎留言评论!
,