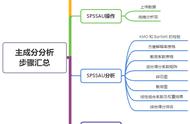
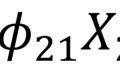从上方可以看到,有几个原始变量,就会得到几个主成分。
实际研究工作中,通常只挑选前几个方差最大的主成分,从而达到简化系统结构、抓住问题实质的目的。
如何求主成分及如何选择主成分?从数学的角度看,求解主成分,其实就是根据数据源的协方差阵,求解特征根、特征向量的过程。
一个结论:主成分可以利用协方差阵的特征值对应的单位正交特征向量来表示。
说明:上述结论其实是一个数学定理,有严格的证明过程,感兴趣的同学可以参考相关书籍。
求出主成分后,如何选择主城分呢?我们引入贡献率,贡献率通过特征根的来表示。

说明:上述λ其实就是特征根。
根据贡献率,一般要求累计贡献率达到80%以上就可以了。当然,这只是一个大体标准,具体选择几个要看实际情况。
从数学角度看,求解主成分的步骤分为以下4步。

因为主成分分析涉及不同指标之间的运算,所以需要考虑数据的标准化。
- 对于度量单位不同的指标或取值范围彼此差异非常大的指标,应该先将数据标准化,然后求协方差阵;
- 对同度量或取值范围在同量级的数据,从协方差矩阵求解主成分。
说明:主成分本来是从协方差阵开始分析,如果从“相关系数矩阵”出发进行分析,相当于将原始数据标准化后,再从协方差阵进行主成分分析,即从相关系数矩阵出发进行主成分分析,则不需要单独进行数据标准化。
实操:利用SPSS进行主成分分析用SPSS进行主成分分析,主要分为以下3步。
1、将数据复制到SPSS中,选择菜单:分析-降维-因子分析,得到以下对话框

说明:SPSS中没有单独的主成分分析选项,通过因子分析(另一种降维分析方法)中的主成分分析进行。
2、“描述”对话框中,勾选“系数”,即给出相关系数矩阵