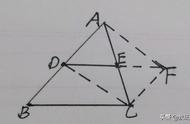
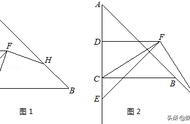
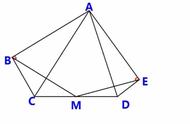
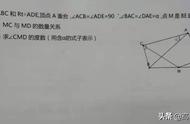
- A中的一个环可以收紧到一个点;B中的一个环被一个孔“卡住”,不能被收紧到一个点。
如果能连续地把一个变形成另一个,然后再变回来,那么这两个流形是同胚的(允许的变形包括拉伸、挤压和扭转,但不允许撕裂和穿孔)。这就引出了著名的甜甜圈和茶杯杯之间的比较(拓补上,它们是同一种东西)。

- 把甜甜圈变形成茶杯
在拓扑学中,我们想对所有流形进行分类,其中在某个类中的所有流形都是彼此同胚的。在二维空间中,很容易看出,如果流形是封闭的且没有洞,那么它就相当于一个2维球体(圆面)。很容易确定一个2维流形是否同胚于2维球体。
庞加莱指出,这在三维中也是成立的,即任何封闭的,单连通的3维流形都同胚于3维球面。
2002年,格里戈里·佩雷尔曼通过使用“里奇流”证明了庞加莱猜想。
P vs NP能否快速验证每个问题是否可以解决,并快速解决?
问题可以分为不同的复杂性类别。这里我们感兴趣的是P和NP类。它们分别表示多项式时间和非确定性多项式时间。
本质上,P问题可以“快速”解决和“快速”验证。而NP问题(目前)并没有一个“快速”的解决方案。更具体地说,给定一个输入大小为n的问题,如果它属于P类,那么求解它所花费的时间根据某个多项式增加。然而如果它是NP,那么它就会增加得更快。
一个被认为是NP的例子是旅行推销员问题的(决策问题):
给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
解决这个问题很困难,也很费力。如果增加城市的数量,将使求解时间的增加比任何多项式都要快得多。
另一方面,一个P问题的例子是验证一个数字是否在给定的列表中。这很容易解决,也很容易检查,如果你将列表的大小翻倍,所花费的时间也会翻倍(所以所花费的时间不会增长得太快)。
P vs NP问题问的是,是否NP问题和P问题是不同的。否则,是否存在一些秘密或隐藏的算法可以快速解决以前认为困难的问题(NP问题)?
纳维尔-斯托克斯问题,存在性和平滑性
在三维空间和时间中,给定初始速度,是否存在一个光滑且具有全局定义的矢量速度和标量压力场来求解纳维尔-斯托克斯方程(Navier–Stokes equations)?
纳维尔-斯托克斯方程是描述三维流体运动的两个非线性偏微分方程。它是两个方程的集合,将速度矢量场和它的变化率与压力场联系起来,也就是作用于液体的外力。方程式是这样写的:

我们不会深入研究每一项的含义,但本质上,第一个方程是牛顿的F=ma。第二个方程也很简单,是质量守恒方程,要求流体不可压缩。
一个“有效”的解有两个条件:
- 向量场v和标量场p是全局定义的,在整个空间上是连续的。
- 总动能是有界的。(v的范数的平方在整个空间上的积分是有界的)。
所以纳维尔-斯托克斯问题可以归结为下面两种情况中的一种:
- 正面表述:给定f = 0和初始速度场(必须满足一定条件),存在满足(1)和(2)的速度场和压力场。
- 反面表述:存在一个初始矢量场和外力场,其中不存在满足(1)和(2)的解。

- N-S方程控制牛奶在茶中的扩散
黎曼函数的所有非平凡零点的实部都等于1/2吗?
让我们分解一下。首先,黎曼ζ函数由下式定义: