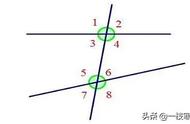
已知:如图①,P点为锐角∠MON内一定点.
要求:在射线OM上找一点A,在射线ON上找一点B,使得△PAB的周长最小.
作图:如图②,分别作P点关于直线OM的对称点P',关于ON的对称点P'',连接P'P''交OM于点A,交ON于点B,点A、点B即为所求,此时△PAB的周长最小,最小值为线段P'P''的长度.
证明:由轴对称的性质可知AP=AP',BP=BP'',△APB的周长AP AB BP=AP' AB BP'',当P'、A、B、P''四点共线时,其值最小.
结论:△PAB的周长最小为P'P''.
4.四边形周长最小

已知:如图①,P、Q为锐角∠MON内的两个定点.
要求:在射线OM上找一点A,在射线ON上找一点B,使得四边形ABPQ的周长最小.
作图:如图②,分别作Q点关于直线OM的对称点Q',P点关于ON的对称点P'',连接P'Q'交OM于点A,交ON于点B,
点A、点B即为所求,此时四边形ABPQ的周长最小,最小值为线段P'Q' PQ.
结论:四边形ABPQ的周长最小为P'Q' PQ.
5.两动两定变式模型

已知:如图①,A、B为两个定点,P、Q为动点.
要求:在射线OM上找一点Q,在射线ON上找一点P,使得AP PQ QB最短最小.
作图:如图②,分别作A点关于直线ON的对称点A',B点关于OM的对称点B',连接A'B'交OM于点Q,交ON于点P,点P、点Q即为所求,此时AP PQ QB最小,最小值为线段A'B'.
结论:AP PQ QB最小为线段A'B'的长.
搭桥模型
模型1

已知:如图①,直线m∥n,A,B分别为m上方和n下方的定点(直线AB不与m垂直).
要求:在m,n之间求作垂线段PQ,使得AP PQ QB的值最小.
解析:PQ为定值,只需要AP QB最小,可通过平移,使P,Q“接头”,转化为基本模型(将军饮马).
作图:如图②,将点A沿着平行于PQ的方向,向下平移至点A',使得AA'=PQ,连接A'B交直线n于点Q,过点Q作PQ⊥n于点Q,交直线m于点P,线段PQ即为所求,此时AP PQ QB最小.
证明:由作图过程可知四边形QPAA'为平行四边形,则QA'=PA,当B,Q,A'三点共线时,QA' QB最小,即PA QB最小,又PQ长为定值,所以此时AP PQ QB的值最小.
模型2