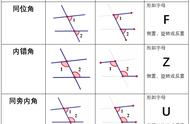
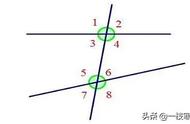
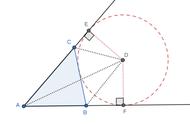
等腰三角形中有底边中点时,常作底边的中线,利用等腰三角形,,三线合一”的性质得到角相等或边相等,为解题创造更多的条件,当看见等腰三角形的时候,就应想到.“边等、角等、三线合一”.
模型3 中位线模型

在三角形中,如果有中点,可构造三角形的中位线,
利用三角形中位线的性质定理:DE//BC,且DE= BC来解题.中位线定理中既有线段之间的位置关系又有数量关系,该模型可以解决角相等,线段之间的倍半、相等及平行问题.
模型4 斜边中线模型

在直角三角形中,当遇见斜边中点时,经常会作斜边上的中线,利用直角三角形斜边上中线等于斜边的-半,即CD= AB,来证明线段间的数量关系,而且可以得到两个等腰三角形:△ACD和△BCD,该模型经常会与中位线定理一起综合应用.
半角模型
模型1 基本模型