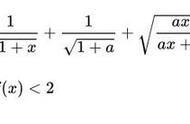1984年高考数学,被称为是中国数学史上最"臭名昭著"的一场数学考试,因为它让全国所有考生都陷入绝望之中,满分120分,北京市的平均分数仅仅只有17分,安徽省的平均分数仅仅只有28分,整个平均分在全国第一的江苏省也仅仅只有49分。而全国的平均分仅仅只有26分。
当年考试一结束,气的许多老师立马发表了期刊文章,表达对那年试题的批评:"我们认为今年高考数学试题不适合高校选拔新生,与现行中学数学教学要求也不吻合,试题偏刁,难度偏高,排列不当,分配不均...",而那年的压轴题更是让所有考生万念俱灰,连参加国际数学竞赛得到名次的考生也有许多没能解出来,在教科书的练习题和习题均未见达到此题要求的题型,查阅建国以来的历届高考试题,也从未达到此题的要求高度,因为其难度,
甚至连苏淳、严镇军、杜锡录、李庆胜等教授名师都研究过此题,其中苏淳教授是这样评价道:“这是一道考查数列的基本知识、不等式的证明和数学归纳法的运用,这道题因为涉及的是非线性递归数列还有许多数列极限的背景,因而难度更大”。
#02
2008年江西省数学高考


2008年,江西省数学高考的最后一道题让无数当年的考生痛哭流涕,因为这道题目全省30余万人无一人能全部答出,而这道题目的难度之大也惊动了当时已经是中国科学院院士的张景中教授。
理科数学卷各主观题平均得分一目了然,而最后一道数学题的分值为14分,但是平均分仅为0.31分。
一个经历过这道数学题的人回忆道:“在我们学校一个公认的数学高手,每次高三数学考试的平均分都在147以上,他高考时在一个小时完成了所有的数学题,接着将画面的一个小时花在了这道题目上,但却毫无结果”。而全省能做出这道题的老师也屈指可数。
#03
2002年高考文科数学